- Get rid of all
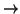 operators.
operators.
- Push the
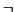 operators in as far as possible.
operators in as far as possible.
- Rename variables as necessary (see the step below).
- Move all of the quantifiers to the left (the outside) of the
expression using the following rules (where
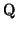 is either
is either
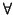 or
or 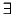 , and
, and 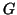 is a formula that does not contain
is a formula that does not contain
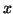 ):
):
-
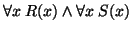 becomes
becomes
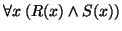 .
.
-
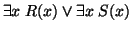 becomes
becomes
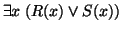 .
.
-
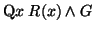 becomes
becomes
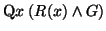 .
.
-
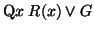 becomes
becomes
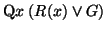 .
.
-
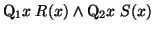 becomes
becomes
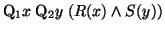 .
.
-
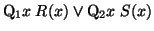 becomes
becomes
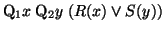 .
.
This leaves the formula in what is called prenex form which consists of a series of quantifiers followed by a quantifier-free formula, called the matrix.
-
- Remove all quantifiers from the formula. First we remove the
existentially quantified variables by using Skolemization. Each
existentially quantified variable, say
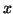 , is replaced by a function
term which begins with a new,
, is replaced by a function
term which begins with a new, 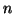 -ary function symbol, say
-ary function symbol, say 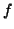 ,
where
,
where 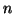 is the number of universally quantified variables that occur
before
is the number of universally quantified variables that occur
before 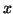 is quantified in the formula. The arguments to the function
term are precisely these variables. For example, if we have the
formula
is quantified in the formula. The arguments to the function
term are precisely these variables. For example, if we have the
formula
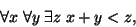
then
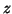 would be replaced by a function term
would be replaced by a function term 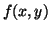 , where
, where 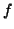 is a
new function symbol. The result is:
is a
new function symbol. The result is:
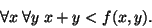
This new formula is satisfiable if and only if the original formula is satisfiable.
The new function symbol is called a Skolem function. If the existentially quantified variable has no preceding universally quantified variables, then the function is a 0-ary function and is often called a Skolem constant.
After removing all existential quantifiers, we simply drop all the universal quantifiers as we assume that any variable appearing in a formula is universally quantified.
- The remaining formula (the matrix) is put in CNF by moving any
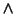 operators outside of any
operators outside of any 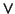 operations.
operations.